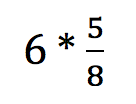The author's daughter has demonstrated exceptional reasoning skills in fractions, going beyond the typical approach taught in school. She used a unique "partial products" strategy to multiply fractions, which the author had never seen before. This approach shows that there are alternative methods beyond the standard algorithm, and that students should be encouraged to develop their own understanding rather than being limited to a single prescribed method.
The author also observed that the daughter used "partial sums" to add fractions, again showing an innovative approach that does not require the use of a common denominator. This suggests that fluency in math should not be solely defined by speed, but also by flexibility, efficiency, and accuracy in problem-solving.
The author emphasizes that memorization of facts and algorithms should not be the ultimate goal in math education, as it can limit a student's long-term understanding and problem-solving abilities. Instead, the focus should be on developing a strong conceptual foundation, which can be built from the early grades and continue to bear fruit in the later years.